Unity中的四元数
unity中,要进行旋转操作的时候,经常用到的是 Transform.Rotate 的方法,例如:
public class Rotator : MonoBehaviour |
这种旋转方式也就是平时经常提到的欧拉角旋转,这种旋转的本质其实是利用了矩阵的乘法。以二维空间为例,我们可以发现,对于二维空间的一个点(我们将它的坐标表示为列向量),对其进行一次矩阵的乘法,可以将其成功的旋转。
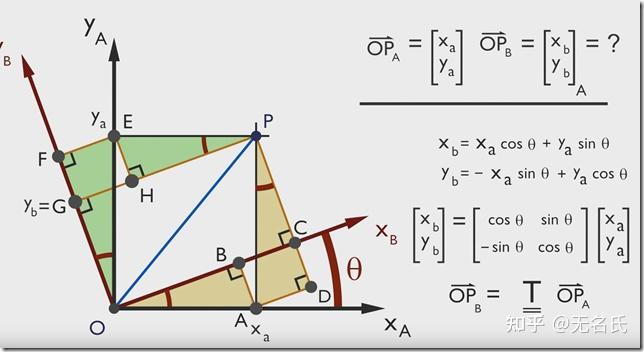
这里的矩阵,实际上就是绕着原点旋转一定角度的旋转矩阵。当然,在实际使用时,为了统一旋转和平移操作,我们会使用齐次坐标表示法来进行延拓,不过这不在我们讨论旋转的范畴当中。
同理,我们可以将其拓展到三维,从而推出分别绕着三个轴的旋转矩阵:

但是,这样的操作是存在问题的,最典型的问题就是万向结死锁的问题,也就是当一个轴旋转了一个角度之后(例如90度),会造成其它两个轴重合的情况,此时如果我们再对两个轴进行旋转操作,会发现结果是一样的,此时我们就会丧失一个维度的旋转。
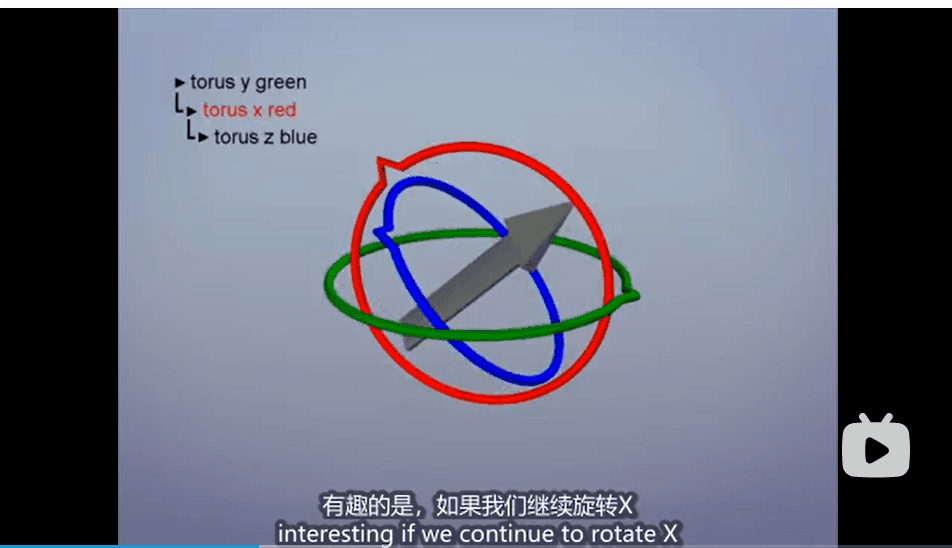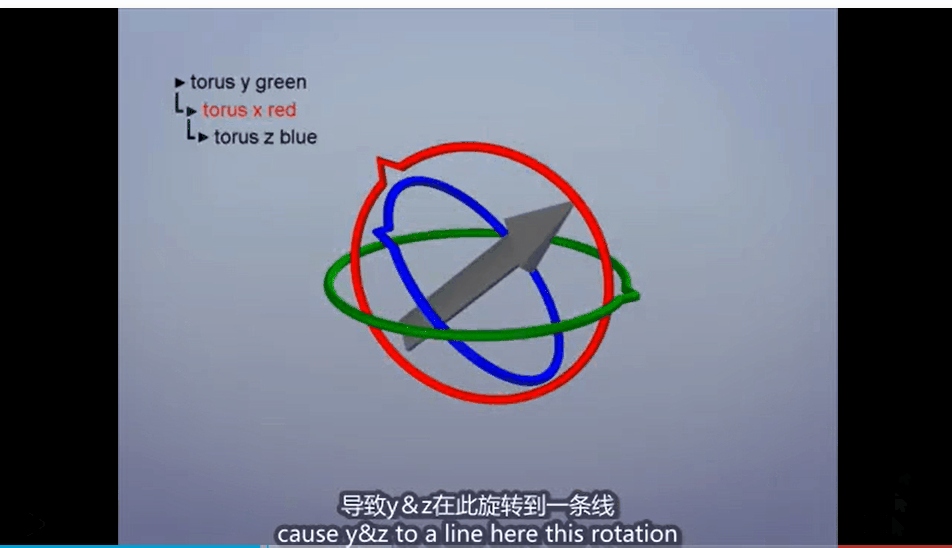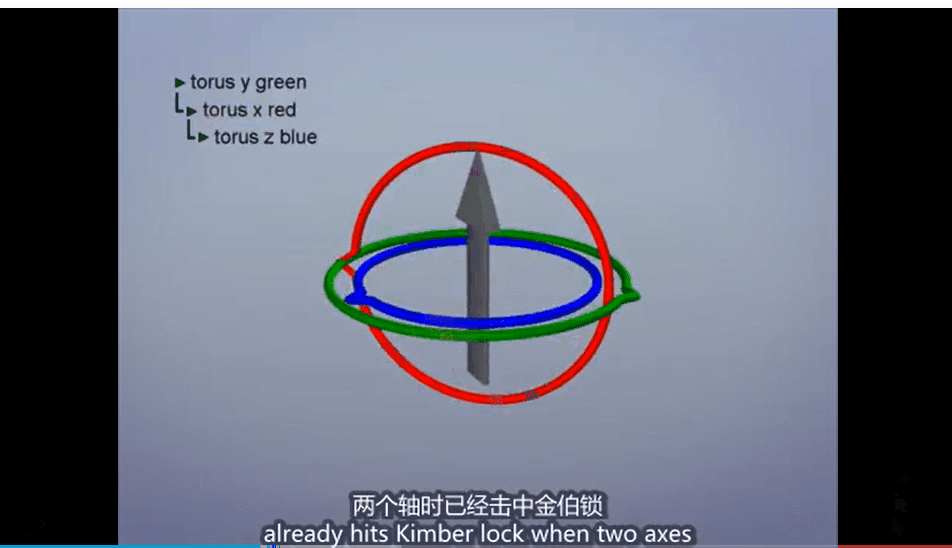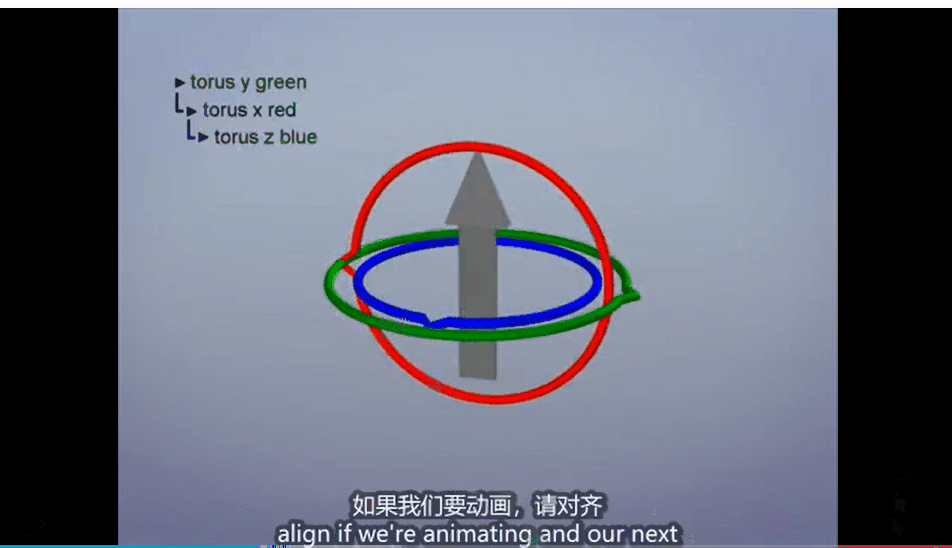
为了解决这个问题,我们就需要引入四元数的概念了。
首先,四元数并不是生来为了解决三维旋转,而是它的性质非常有利于表达旋转信息(后面会详述),所以了解四元数的性质要先于了解四元数在旋转中的应用。至于四元数替代欧拉角等形式,就需要牵扯到一些别的知识点,我先罗列一下四元数相比其他形式的优点:
- 解决万向节死锁(Gimbal Lock)问题
- 仅需存储4个浮点数,相比矩阵更加轻量
- 四元数无论是求逆、串联等操作,相比矩阵更加高效
所以综合考虑,现在主流游戏或动画引擎都会以缩放向量+旋转四元数+平移向量的形式进行存储角色的运动数据。
我们先看一下欧拉公式:
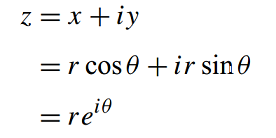
正如复数是有一个实部和一个虚部组成的,那我们将一个虚部换成三个虚部,即两两相交{i, j, k}。
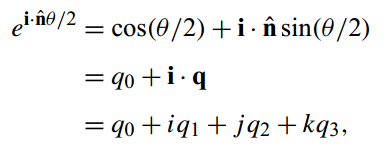
其中n为三维的单位向量,i²=j²=k²=i·j·k=-1。这便是四元数的常规表达形式,不过单位四元数是有一大堆的约束的,并不是所有四维向量都是四元数。
(待更新)
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 YEAGER在海的那边的小木屋!
评论